Лекция II. Физика воды для инженеров и механиков

ГК Гидросервис любит радовать своих покупателей не только приятными акциями и плюшками, но и интересным, познавательным материалом для размышления и чтения. Мы продолжаем публиковать научно-популярные статьи, написанные Когтевым Н.В. Они написаны настолько популярным языком, что вся наука, представленная читателю, становится ясной и понятной, как дважды два — четыре. Желание хоть как-то откорректировать представление о воде, важнейшем теплоносителе, растворителе, главном материале нашего устройства, в основном потребляемом нами продукте в конце концов, посвящены две эти лекции.

Итак, формула:

Δ(Р)Δ(V) < kT

где k - постоянная Больцмана.

§5

Современные представления структуры воды

Важнейшим новым и весьма современным представлением является понимание того факта, что жидкая вода является сложным раствором, состоящим из множества компонентов. Конечно же это представление появилось не сегодня. Всё началось с неизвестного ещё в ту пору (1892 г.) Вильгельма Конрада Рентгена. Была к той поре уже написана и диссертация Менделеева, но кто у нас читает диссертации? Тогда ведь русский язык тоже не был языком науки.

Конечно после присуждения В. К. Рентгену звания Нобелевского лауреата №1 по физике, написанные им статьи были прочитаны. В. К. Рентген предположил, что в жидкой воде должны присутствовать осколки ледяной структуры и с повышением температуры к пару их количество уменьшается.

Рентген позже увлёкся Х-лучами, а к намеченной, но брошенной им, теме подключилась огромная армия исследователей, создавшая горы познавательной литературы, изобилующей превосходными степенями: уникальная, аномальная, парадоксальная вода. Детали этого продвижения и имена участников (громкие и не очень) мы здесь пропустим и передадим их истории науки.

Что же сегодня известно? Рассмотрим 1Н₂О¹⁶

Близкий к шаровой форме, атом кислорода шестнадцатого, про пространственную ориентацию которого нам не известно почти ничего, сильно искажается прильнувшими к нему двумя атомами водорода.

Поневоле вспоминаешь академика Грибова: «…не люблю я молекулы — кривые они очень!..». Шар становится похож на камень: есть две области пониженной плотности электронного облака и две, почти сросшиеся в одну, повышенной плотности электронного облака. Молекула стала уже чётко пространственно-ориентирована. Заметен и дипольный момент размером в 1 дебай. Но если заполнить такими камнями литровую банку, то при плотной упаковке весить она будет более одного килограмма восемьсот граммов. Значит есть ещё и то, о чём начал говорить В.К. Рентген.

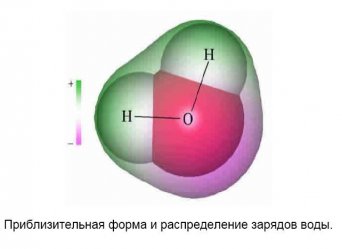
Понятие водородная связь было введено У. Родебушем в 1920 году для объяснения разрыхления воды. Суть в следующем:

Молекулы воды за счёт «дефектов» плотности электронных облаков взаимодействуют друг с другом, образуя вид связи отличный от ковалентного и чисто вандервальсового. Будучи всё же химической, водородная связь только лишь в 10% случаев приводит к обмену электронов разными молекулами. В остальных случаях молекулярные облака остаются строго индивидуальными, а связь имеет четко Кулоновскую природу. А коли так, то длина водородной связи так же не остаётся постоянной, а зависит от внешнего окружения. Не строго фиксируется и угол ~104 градуса. Поэтому различна энергия связи. К этому ещё предстоит вернуться. Но важно понять, принять и впредь не сомневаться:

Молекулы воды, объединённые водородной связью образуют энергоёмкий каркас, болтающийся среди молекулярной воды и себе подобных, составляя динамическую систему, полностью соответствующую понятию — раствор.

Реакция образования водородной связи — реакция экзотермическая, реакция распада водородной связи — реакция эндотермическая. Энтальпия этой реакции составляет по разным оценкам от 4 до 20 ккал/моль. Понятно, что для разрушения каркаса сцепившихся молекул, нужна энергия. Этой энергией является кинетическая энергия компонентов раствора, т.е. температура.

Обратите внимание на занимательную картинку: каркас массивнее в несколько, в сотню раз одиночной молекулы. Посмотрите на процесс присоединения одиночной молекулы к каркасу. Прилипающая к каркасу, возбуждённая в температурном смысле молекула, передает своё возбуждение каркасу, а тот в свою очередь возвращает его (возбуждение) в раствор остальным участникам. Температура раствора растёт. А стабильность каркаса уменьшается.

И обратный процесс (таяние льда) — испытывая лишнее, в энергетическом смысле, напряжение, каркас отбрасывает одну молекулу и становится в более выгодную в энергетическом плане позицию, он становится менее энергонасыщенным и более стабильным. А «температура» каркаса падает! И потребуется время, чтобы соседи набрали мощи и его вновь дообеспечили его энергией для последующего сброса лишнего.

Приведенная картинка прежде всего свидетельствует, что при таянии льда или распаде ассоциата, процесс освобождения молекул от ледяного осколка идёт ступенчато и пропорционально имеющемуся — т.е. экспоненциально!

N=N0e-λt

где λ = f(Т°)

Освободившаяся от связи молекула подчиняется известному закону — отсутствия последействия, т.е. она не помнит о своём прошлом! Здесь кроется радикальное отличие водородной от металлической связи.

В большинстве веществ молекулы удерживаются в узлах своих кристаллических структур вандервальвовыми или электрическими силами. В ассоциатах связь водородная – она значительно сильнее, а самое главное — она строго направленная! Это приводит к тому, что при плавлении льда ли, при отрыве от ассоциата ли, она рвётся только сразу. Водородная связь не может ухудшаться постепенно, прежде чем порвётся. Либо - либо.

Смотрите на кристалл большинства иных веществ при нагревании:

1. Усиливается тепловое движение молекул,
2. Молекулы начинают отклоняться от своего положения, разъезжаться из узлов всё дальше и дальше, но, внимание! связи сохраняются.

Что происходит с молекулой воды оторвавшейся от каркаса?

До отрыва молекула связана со своими соседями связями, ориентированными в строго определённую точку пространства. И если она оторвалась, то ориентиры потеряны, и возврата в прошлое положение нет! Оторванная молекула не может замкнуть свои два протона и два неподелённых электрона. Молекула воды, оторвавшись, порвала со своим прошлым сразу и бесповоротно.

Даже кажется, что и памяти у воды быть не может. Но выше уже говорилось, что отрыв одной молекулы приводит к повышению прочности остального каркаса. И не может быть такой энергии, что б разорвать все связи каркасного ассоциата разом! Только поэтому память и остаётся. Сравнивая процессы охлаждения (замерзания) и нагрева (таяния) мы видим, что продуктивность первого процесса выше, чем у второго. В первую очередь это связано с перераспределением внутренней энергии раствора. При охлаждении всего раствора ещё не вовлеченная в ассоциат молекула становится более подвижной и у неё больше шансов подскочить к ассоциату с «правильной» ориентацией.

В этом кроется разгадка известного эффекта Эрасто Мпемба — горячая вода замерзает быстрее холодной.

Создавая больший температурный градиент на границе системы, мы обрекаем раствор на большую скорость формирования структуры. Мы же часто видим в футболе, особенно в играх английской премьер лиги, как при равном профессионализме исход игры зависит (грубо) от подвижности игроков на поле.

Мне уже приходилось писать о теплогенераторе Потапова. Вот уж лучшего макета для демонстрации водородной связи и придумать нельзя. Закрученный в трубе поток воды, увеличивает давление в пристенных областях за счет силы инерции. Возникают условия для интенсивного роста каркасных ассоциатов в сжатом инерцией слое. Чем выше давление, тем больше становится каркасных ассоциатов, температура растёт вслед. На выходе из трубы вода перегрета сверх расчёта. Но дайте ей время, и она сама вернётся в исходное состояние, может быть даже став холоднее первоначальной. Всё зависит от тех тепловых потерь, какие она –вода - понесёт при течении по трубам.

Известна холодная резка металла и камня сверхсжатой (до 400 атм.) струёй воды.

Не становится ли Вам ясно, уважаемый читатель, за счёт какого абразива режет струя? А ведь этот абразив по происхождению родственник алмазной крошке... Понимание воды как раствора различных ассоциатов, длиной подчас до тысяч молекул, существенно облегчает понимание процесса резания, тем паче, что сходственный процесс – пескоструй - всегда можно посмотреть.

А помните вихревые нити Гельмгольца?

Не сможет ни один каркасный ассоциат в растворе быть неподвижным! Как уже было сказано выше: кривой он очень. Начав вращаться при оттаивании, он остановится только в одном случае — когда вновь замёрзнет! Видимо потребуется время на осознание того, что ламинарное течение -  есть вырожденное состояние турбулентного, а не наоборот.

Об Эренфестовых масштабах и временах

Осталось понять, почему изложенное модельное представление столь долго к нам не приходило? Отвечу, памятуя Шопенгауэра, следовало подождать пока вырастет поколение знающее, что такое 25-й кадр. Мне могут возразить, что и две тысячи лет тому назад люди знали, что бесполезно, выступая перед толпой, говорить истину. Надо рассказывать притчи. Тогда кто-нибудь поймёт, или по крайней мере, запомнит изложенное. С притчами инженеру сложно, а вот поколению, посещавшему кинотеатры на премьеры Чапаева или Фантомаса, уже хорошо известно, что между кадрами на плёнке есть пробел, перемычка, граница между кадрами.

И от того насколько правильно на непрерывном процессе поставлены эти пробелы зависит понимание происходящего на экране. Первым в технике это понял и озвучил Пауль Эренфест.

Всякому явлению есть свой временной масштаб.

Рассмотрим временные масштабы жизни каркасных ассоциатов. Частота Дебая = 1013, значит время наблюдения одиночной молекулы воды (время жизни) =10-13 секунд, время жизни диполя = 10-12 секунд, время жизни случайного ассоциата =10-11 секунд, время жизни каркасного ассоциата =10-10 секунд.

Данные эти расчётные, следует читать их с точностью до порядка. Большая точность для понимания сегодня вряд ли потребна. Приведённые значения времён жизни ассоциатов прежде всего говорят о том, что без применения специальных методов их невозможно увидеть. Частота мерцания кадров в четыреста миллионов раз больше, чем на кинопленке. Но разглядывать их уже умеют. А люди столь же творческие сколь и маргинальные, рисуют картины более красивые, чем фуллерен 60.

Смотрите у Мартина Чаплина:

На приведенном рисунке молекулы представлены в виде шариков, что так же не верно. На самом деле подобная идеализация бесконечно далека от жизни.

На этапе услышанного и понятого очень сложно удержать себя от попыток упрощенной математической формализации динамического процесса в нашем растворе. Собственно, это обстоятельство и послужило тормозом развития теории воды по Рентгену. Прагматичное желание последователей, подхвативших саму идею осколков, наворочать формул с линейными (или эспоненциальными) зависимостями, завело красивую идею в тупик.

Вернемся к идеализации, изображенной на первом рисунке, о распределении зарядов в молекуле воды. Следует ещё раз подчеркнуть, что водородная связь имеет главным образом Кулоновскую природу. К сегменту высокой плотности электронов, занимающему 90 градусов, примкнуть удаётся обыкновенно двум протонам соседней молекулы. Но всегда могут быть примыслены условия, когда этих протонов может быть и один, и три, а возможно и больше. Всё зависит от соседей, их положения в пространстве, заряда, расстояния.

У Валерия Брюсова в его стихотворении «Мире электрона»  читаем:

Там всё, что здесь в объёме сжатом,
Но также то, чего здесь нет.
Их меры малы, но всё та же их бесконечность как и здесь;
Там скорбь и страсть как здесь, и даже Там та же мировая спесь.

Искушение процитировать полностью велико, но пора и честь знать.

При большем количестве протонов (скажем три на один кислород) увеличится длина связи и уменьшится её прочность. В совершенно определённых пределах, энергия связи и её длина - вещи настолько взаимосвязанные, что термины можно считать синонимами.

§6

О внутренней энергии

Рассмотрим некий элементарный объём воды вне каких-либо внешних воздействий в условиях жидкой воды при давлениях близких к атмосферному. Полная внутренняя энергия этого объёма состоит из кинетической энергии U_кин. молекул, энергии связи молекул в ассоциатах U_св., и, собственно, внутренней энергии молекулярной воды U_мол., включающая химическую, атомную и ядерную составляющие. Обозначая Е_вн. - полную внутреннюю энергию, можем записать:

U_кин. + U_св. + U_мол.= Е_вн. (1)

U_мол. - при условиях нашего рассмотрения величина неизменная, как и Е_вн., поэтому можем записать:

U_кин. + U_св.= Const (2)

Как видно было ранее из нашего рассмотрения частоты изменения U_кин. и U_св. настолько велики, что можно полагать эти функции непрерывными.

Продифференцировав выражение (2) по времени Т имеем:

dU_кин./dТ = -dU_св./dТ (3)

U_кин. — кинетическая энергия молекул, из курсов физики =1/2 mмv2 m =3/2 kT

U_св. — энергетический запас аккумулированный во временных, каркасных и прочих ассоциатах, образованных водородными связями.

Обозначим Q_моль количество энергии, которым обладает 1 моль воды структурированной воды за счёт водородной связи. По разным данным это от 4 ккал до 20 ккал на моль.

Тогда энергия, приходящаяся на одну молекулу равна Q_моль/N_{авогадро}. Безусловно речь идёт о средних значениях.

Запишем это в виде формулы: 3/2 kdT/dТ = -Q_моль/N_{авогадро} dN/dТ, сгруппировав постоянные коэффициенты имеем: dT/dТ = -СdN/dТ или

dT/dТ + СdN/dТ = 0 (4),

где С = 3/2 k N_{авогадро} / Q_моль

§7

Анализ полученного результата

dT/dТ + СdN/dТ = 0

Нами получено важнейшее уравнение, отражающее динамические процессы, происходящие в элементарном объёме чистой воды.

Важно осознавать, что процессы эти:

1. Непрерывны,
2. Постоянны,
3. Обратимы.

В элементарном объёме чистой воды всегда идёт процесс поддержания динамического равновесия между компонентами, составляющими саму воду. Этот процесс чутко реагирует на малейшие изменения внешних воздействий. (10-13 сек.), например, на действие консервативных сил.

Внедрение же в рассматриваемую нами воду скажем 1 атома благородного газа уже меняет равновесие — это другой! раствор. Не повторяйте ошибок Прандтля! Становится понятно, что физические свойства двух вод: охлажденной до температуры Т= Х₀ и нагретой до той же температуры при одном и том же давлении — разные, но стремящиеся к одинаковому значению. А вот время сближения значений зависит от множества факторов!

И с этим ещё предстоит разобраться…

Библиография

1. «Айрес», фонд развития новых медицинских технологий, материалы сайта www.aires.spb.ru, 2005
2. Высоцкий В.И., Корнилова А.А. Физические основы долговременной памяти воды. - Вестник МГУ, серия 3, Физика, 2004, №3
3. Ефимов Ю.Я. Симметричны ли молекулы Н2О в жидкой воде? - Институт химической кинетики и горения СО РАН, Новосибирск, Электронный журнал «Исследовано в России», http://zhurnal.ape/relarn/ru/articles/2001/123.pdf
4. Зеленин Ю.М. Двухкомпонентная модель структуры воды. - Электронный научный журнал «Исследовано в России», http://zhurnal.ape.relarn.ru/articles/2005/110/pdf
5. И. де-Бур. Теория жидкого состояния. -Успехи физических Наук, том LI, вып. 1, 1953
6. Карапетьянц М.Х., Дракин С.И. Общая и неорганическая химия. - Учебник, 3-е изд., М., Химия, 1994
7. Малафеев Н.Т. О природе возникновения изогнутых связей в воде. - Письма в ЖТФ, том 29, вып. 1, 2003
8. Слесарев В.И., Шабров А.В. Влияние структуры воды на её статические и динамические свойства. - Вестник СПб ГМА им. Мечникова, 2000
9. Справочное руководство «Химия» под ред. Г. Койне, Л., Химия, 1978
10. Стебновский С.В. О сдвиговой прочности структурированной воды. - Журнал Технической Физики, том 74, вып. 1, 2004
11. Стебновский С.В. Журнал Технической Физики. - 2002, том 72, вып.11, с. 24-27
12. Френкель Я.И. Теория жидкого состояния. - Издательство «Правда»,  М., 1948
13. Цирельсон В.Г. Химическая связь и межмолекулярные взаимодействия. - Конспект лекций по квантовой химии, РХГУ им. Д.И.Менделеева, М., 2004
14. Шапошник В.А. Анализ температурной зависимости вязкости воды. - Вестник ВГУ, Воронеж, №1, 2004, с. 107-109

Комментарии:

Добавить комментарий